点分治 - 学习笔记 <未完>

壹

学习网站：OI Wiki yxc的生动讲解

Pro：P3806 P4178 P6329

贰

2.1

首先，用人话来讲，就是一个树上的分治思想。

但是本人之前学分治的时候没有沉淀，导致理解不透彻，所以再赘述一遍分治思想：

分治（英语：Divide and Conquer），字面上的解释是「分而治之」，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

人话说就是：有一个巨大无比的蛋糕，你想知道他不同部分的不同味道，于是乎不停切，最后每个小块切成可以一口一个的大小，然后每个不同部分吃掉一个小块。

其实最主要就记住 分而治之，然后性感理解一下。

（不性感理解一下的话，到时候写代码的时候，对于 分 的 递归（推），治 的 归并 就会感到一头雾水）

2.2

2.2.1

那么点分治也就是拿点来切树。边分治同理，但会被菊花图卡掉（时间会假到 $ n^2 $ 去），所以这里就不提了。

那么这个拿来切树的点，自然有讲究。

我们为了保障时间的复杂度，所以就选择一个类 重心 的点作为根来切树。它需要满足 任意一个它的子树，其节点数 不超过 总节点数 的 $ \frac 1 2 $。那么如果以这样的点进行 dfs 的话，就可以有如下图的结构，将总问题分治至若干子树分别求解。

为什么不找重心，而找一个类重心点？ 因为我们找这个点来 dfs，只是为了降低时间复杂度，代替每个点都搜一遍的方法。所以只要某点满足上述条件，就可拿来作为根进行 dfs。

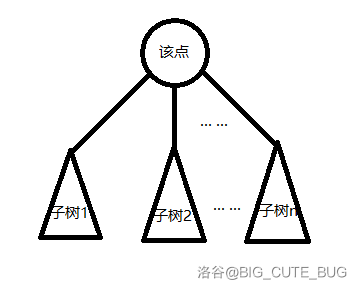
这个点分治思想，会不断 分 进每个子树内部，再如上述找一个 类重心点，继续 分。对此，递归的时间复杂度，最坏情况是，每个子树大小 恰好为 总节点数 的 $ \frac 1 2 $，也就是一棵二叉树，会递归 $\log n$ 层，其为 $ \log{n} $ 的复杂度；而最好情况则是，每个子树大小 恰为 $ 1 $，会递归 $1$ 层，其为 $ 1 $ 的复杂度。

而找根总共会将整棵树遍历，所以是 $\Omicron (n)$。

其中每 分 一次 治 一次，分完最后归并答案。对这个 治 的过程的时间复杂度来讲，每层分治都会处理 $n$ 个点，所以会有 $n$ 的复杂度。

上面三者结合后可得出点分治的时间复杂度为：$ \Omicron (n {\log} {n}) \text{ 与 } \Omega (n) $

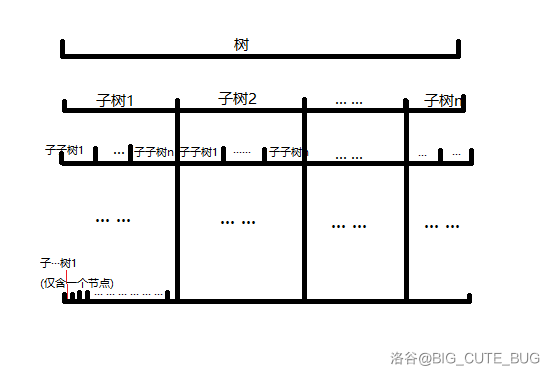
（这是点分治的递归层数示意图 （有点抽象罢了）

另外，当下点分治是 树上路径 问题处理的热门方法。

2.2.2

接下来结合实际例题分析点分治思想的运用以及细节处理。

例题1 P4178

给定一棵 $n$ 个节点的树，每条边有边权，求出树上两点距离小于等于 $k$ 的点对数量。

这里就先分析用分治来做的大框架。

首先找到某类重心点，以该点作根。这里找点可以 dfs 去找，其中具体实践主要是，搜到某点时，按照根需满足的性质，来判断该点是否可作为根。

然后，对满足条件的点对进行分析，发现通过求解方式可分为三类点对：

1. 点对在此根下的同一子树内

2. 点对其中之一即该根

3. 点对在此根下的不同子树内

那么对应点对数量的求解方式为：

1. 分 到子树里去 治，最后归并回本层时加上就行了。

2. 对某个子树，dfs 找出该子树内节点至该根的距离，若满足条件则答案加一。

3. 显然这类点对，两点间距离为，各自到该根距离之和。也就可以通过第二类中算出的距离来计算个数。

另外：

• 对于第二类，具体来讲

  1. 可在代码中遍历子树节点距离来判断。

• 对于第三类，具体来讲

  1. 可以采用容斥原理，用该根下满足 条件 的所有节点，减去其中的非法情况（即两点在同一子树内的点对数量）。

  2. 可以对该子树内所有点至根的距离排序，然后双指针扫一遍算出某子树内，满足第三类 条件 的点对数量。且双指针有些细节需注意，这里将在代码中表明。

     • 第三类的条件指：两点各自到该根距离之和，小于等于 $ k $。

• 每当找出一个根后，需标记该点已走。

以及其复杂度。首先是点分治思想本身的 $n\log n$。然后每层递归，每个点都会被记录一次到某一根的距离，因此每层排序复杂度为 $n\log n$，再加上共有 $\log n$ 层，所以排序总复杂度为 $n \log^2 n$。同理，每层递归的双指针复杂度总共为 $n$。故三者合并，即有算法总复杂度 $ \Theta (n \log n + n \log^2 n + n) $。

以上是总体思路，接下来是代码实现。

找类重心点作根（细节较少，较好实现）：

• get_size 作用是递归分治找根时，将现在正在处理的子树的 total size 传入 ts 参数。

• get_root 的返回值是正在处理的子树的大小。其实就是为了方便判断，而在 dfs 时，将子树大小一并求出，而非每次都去 get_size。

• sum 就是正在处理的子树的大小。注意初始值为 1，要包括当前节点。

• root 直接传入地址，求出后直接将根储存在原变量中。

int get_size(int u, int fa)
{
	int sum= 1;
	for(auto v : e[u])
		if(!vis[v] && v!= fa)
			sum+= get_size(v, u);
	return sum;
}
int get_root(int u, int fa, int ts, int& root)
{
	int sum= 1, ms= 0;
	for(auto v : e[u])
		if(!vis[v] && v!= fa)
		{
			int t= get_root(v, u, ts, root);
			ms= max(t, ms);
			sum+= t;
		}
	ms= max(ms, ts- sum);
	if(ms<= (ts>> 1)) root= u;
	return sum;
}

算子树中节点，距本根的距离：

• v.first 存 $v$ 节点编号，v.second 存边权 $w$。

• 因为用不到节点编号，所以只将所有距离存入数组 p

void get_dis(int u, int fa, int dis, int& qt)
{
	q[++qt]= dis;
	for(auto v : e[u])
		if(!vis[v.first] && v.first!= fa)
			get_dis(v.first, u, dis+ v.second, qt);
}

算某节点距离集合中，满足三类条件点对数量的双指针：

• while 中判断是 j+ 1，意思是：如果 j 能往后走，才往后走。

• j= min(i, j) 作用是：因为 $j>i-1$ 的情况此前已经算过了，所以不重复就取 $min$。

• res+= j 实际加的是从 a 的起点到下标 j 的元素个数。

int get(int a[], int len)
{
	int res= 0;
	sort(a+ 1, a+ len+ 1);
	for(int i= len, j= 0; i> 0; i--)
	{
		while(j+ 1< i && a[j+ 1]+ a[i]<= k) j++;
		j= min(j, i);
		res+= j;
	}
	return res;
}

总计算函数：

• if(!vis[v.first]) 因为到 u 的父节点一定已被 vis 标记，所以只判 vis，就可以不走回去。

int calc(int u)
{
	int res= 0;
	get_root(u, 0, get_size(u, 0), u);
	vis[u]= 1;

	//第三类点对
	int pt= 0;
	for(auto v : e[u])
		if(!vis[v.first])
		{
			int qt= 0;
			get_dis(v.first, u, v.second, qt);
			res-= get(q, qt);
			for(int i= 1; i<= qt; i++)
			{
				if(qt[i]<= k) res++;//第二类点对
				p[++pt]= q[i];
			}
		}
	res+= get(p, pt);

	for(auto v : e[u]) if(!vis[v.first]) res+= calc(v.first);//第一类点对
	return res;
}

record

例题二 P3806

给定一棵有 $n$ 个点的树，询问树上距离为 $k$ 的点对是否存在。

其实两题大同小异，一个是从 小于等于 $k$ 变成了 等于 $k$；一个是变成了多测；再一个是从 个数 变为了 存在。